Limits

In the study of calculus, understanding the concept of a limit is a stepping stone towards delving into continuous functions, derivatives, and integrals. The formal definition, often referred to as the $\epsilon$-$\delta$ definition, is important yet can initially seem impenetrable. These are my notes on the formal definition of limit aimed towards building an intuitive understanding.

Formal Definition

The formal definition of limit hinges on the notions of arbitrarily small quantities, encapsulated by Greek letters $\epsilon$ (epsilon) and $\delta$ (delta). Given a function $f(x)$, the statement

$$\lim_{{x \to a}} f(x) = L$$

is interpreted as: for each small number $\epsilon > 0$, there exists a number $\delta > 0$ such that if $0 < |x-a| < \delta$, then $|f(x) - L| < \epsilon$. In a more symbolic notation, this is articulated as:

$$\forall \epsilon > 0, \exists \delta > 0 : 0 < |x-a| < \delta \Rightarrow |f(x) - L| < \epsilon$$

The crux of this definition lies in the quantifiers. It's about guaranteeing that $f(x)$ gets arbitrarily close to $L$ as $x$ approaches $a$, by making $\delta$ small enough.

Dissecting the Formalism

Let's dissect the components of this definition:

1. The Limit Point ($a$): This is the point that $x$ is approaching.
2. The Limit Value ($L$): This is the value that $f(x)$ is approaching as $x$ approaches $a$.
3. The Epsilon ($\epsilon$): Represents how close $f(x)$ is to $L$.
4. The Delta ($\delta$): Represents how close $x$ is to $a$.

The inequalities $0 < |x-a| < \delta$ and $|f(x) - L| < \epsilon$ are crucial as they formalize the notion of "closeness".

Bridging to Intuition

The $\epsilon$-$\delta$ definition at first might seem detached from intuition. However, a geometric interpretation can provide a clearer picture.

Geometric Interpretation

Imagine a graphical representation where the function $f(x)$ is plotted against $x$. The point $x = a$ is where we are focusing, and $L$ is the value that $f(x)$ is approaching. Now, envision two horizontal lines at $L + \epsilon$ and $L - \epsilon$. Similarly, draw two vertical lines at $a + \delta$ and $a - \delta$. The essence of the definition is that as $x$ moves within the vertical bounds, $f(x)$ stays within the horizontal bounds.

A figure illustrating this geometric interpretation can greatly aid in understanding. The figure would show the function $f(x)$, the point $x=a$, the value $L$, the $\epsilon$ and $\delta$ bounds, and how $f(x)$ remains within the $\epsilon$ bounds as $x$ is within the $\delta$ bounds around $a$.

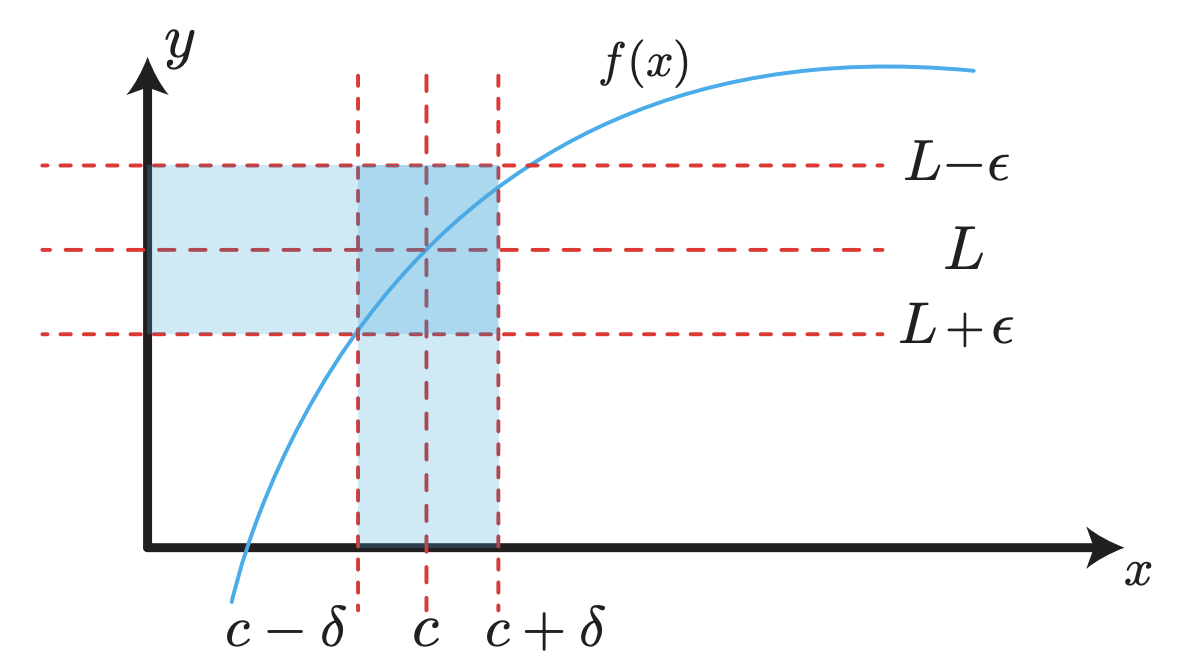
Concrete Scenario

Consider a real-world scenario where a car's speedometer approaches a certain speed as the car accelerates. Though the needle might never hit the exact speed due to mechanical limitations, it gets arbitrarily close. This scenario mirrors the behavior of limits, where $f(x)$ gets arbitrarily close to $L$ as $x$ gets arbitrarily close to $a$.

Through this blend of formalism and intuition, the concept of limits becomes less daunting, serving as a solid foundation for further exploration in calculus.

Certainly. Here’s a section on the formal definition of a limit as ( x ) approaches infinity:

---

Limit as ( x ) Approaches Infinity

In calculus, the concept of a limit is a fundamental building block that underpins many other concepts such as continuity, differentiation, and integration. When we talk about the limit of a function as ( x ) approaches infinity, we are discussing the behavior of the function as ( x ) grows without bound.

Formal Definition

The formal definition of a limit as ( x ) approaches infinity is given as follows:

For a given function ( f(x) ), we say that the limit of ( f(x) ) as ( x ) approaches infinity is ( L ) if for every real number ( \varepsilon > 0 ), there exists a real number ( M ) such that for all ( x > M ), the absolute difference between ( f(x) ) and ( L ) is less than ( \varepsilon ). In mathematical notation, this is expressed as:

$$\lim_{{x \to \infty}} f(x) = L \quad \text{if and only if} \quad \forall \varepsilon > 0, \, \exists M \, \text{such that} \, x > M \implies |f(x) - L| < \varepsilon$$

Interpretation

This definition encapsulates the idea that as ( x ) becomes arbitrarily large, the function ( f(x) ) approaches the value ( L ). The variable ( \varepsilon ) represents how close we want ( f(x) ) to be to ( L ), and ( M ) represents a point beyond which all function values ( f(x) ) are within ( \varepsilon ) of ( L ).

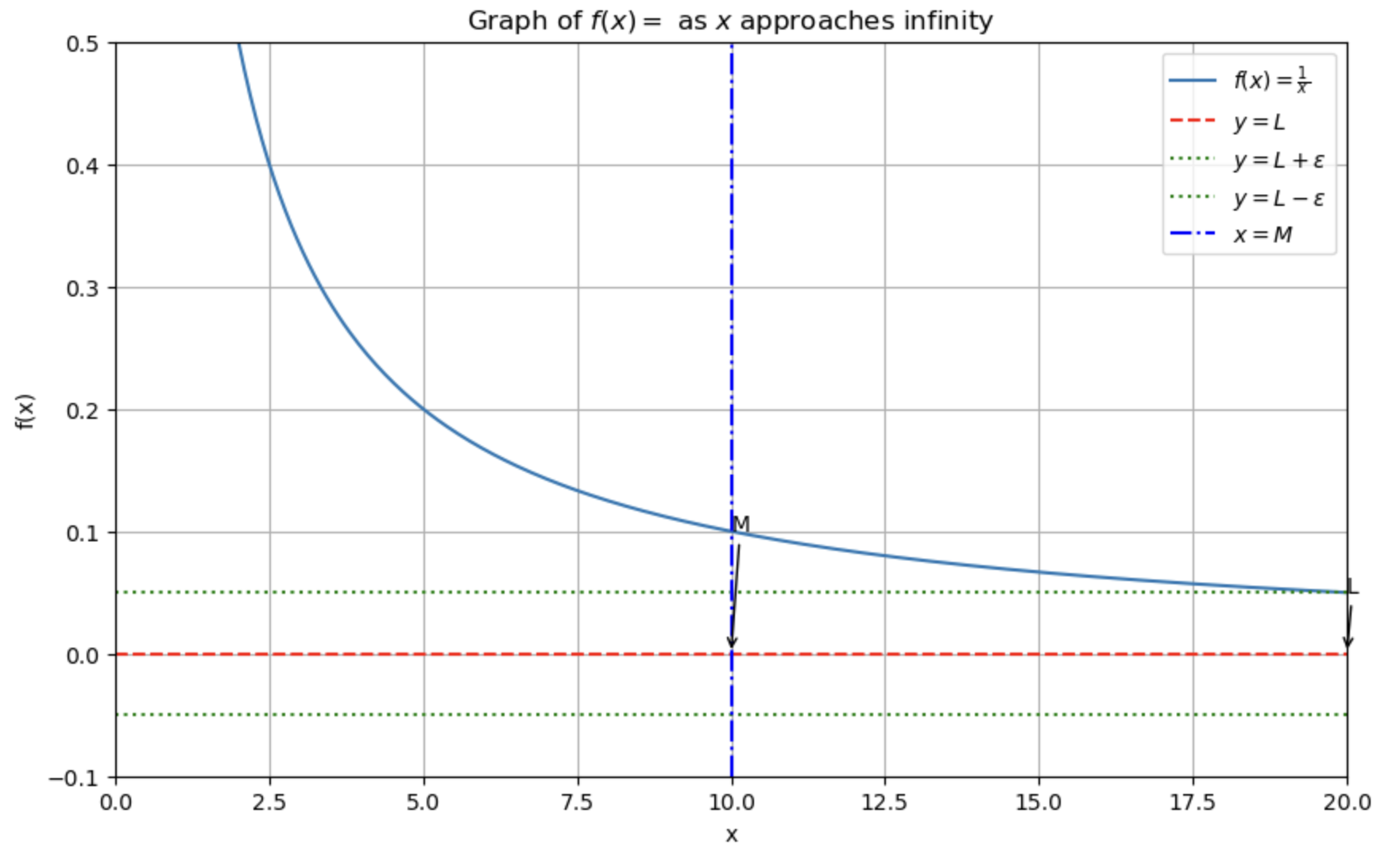
Python Code

import matplotlib.pyplot as plt import numpy as np

# Define the function f(x) = 1/x
x = np.linspace(1, 20, 400)  # Generate x values from 1 to 20
f_x = 1/x  # Compute f(x)

# Define the limit L and epsilon
L = 0
epsilon = 0.05

# Define the value of M (choose M = 10 for this example)
M = 10

# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(x, f_x, label=r'$f(x) = \frac{1}{x}$')
plt.axhline(y=L, color='r', linestyle='--', label=r'$y = L$')
plt.axhline(y=L + epsilon, color='g', linestyle=':', label=r'$y = L + \epsilon$')
plt.axhline(y=L - epsilon, color='g', linestyle=':', label=r'$y = L - \epsilon$')
plt.axvline(x=M, color='b', linestyle='-.', label=r'$x = M$')

# Annotate M and L
plt.annotate(text='M', xy=(M, 0), xytext=(M, 0.1), arrowprops=dict(arrowstyle='->'))
plt.annotate(text='L', xy=(20, L), xytext=(20, L + 0.05), arrowprops=dict(arrowstyle='->'))

# Set plot limits and labels
plt.xlim([0, 20])
plt.ylim([-0.1, 0.5])
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Graph of $f(x) = \frac{1}{x}$ as $x$ approaches infinity')
plt.legend()
plt.grid(True)
plt.show()

---

Questions

Question 1

Prove ( \lim_{{x \to 3}} (2x + 1) = 7 )

To prove the statement ( \lim_{{x \to 3}} (2x + 1) = 7 ) using the epsilon-delta definition, we need to show that for every ( \varepsilon > 0 ), there exists a ( \delta > 0 ) such that if ( 0 < |x - 3| < \delta ), then ( |(2x + 1) - 7| < \varepsilon ).

Let's breakdown the steps:

1. Expression Simplification: Simplify the expression ( |(2x + 1) - 7| ): [ |(2x + 1) - 7| = |2x - 6| = 2|x - 3| ]

2. Epsilon-Delta Relation: Now, we need to find a ( \delta ) such that ( 2|x - 3| < \varepsilon ) whenever ( 0 < |x - 3| < \delta ). It's clear from the expression that if we choose ( \delta = \frac{\varepsilon}{2} ), the inequality will be satisfied: [ 2|x - 3| < \varepsilon ]

3. Formal Proof: For every ( \varepsilon > 0 ), choose ( \delta = \frac{\varepsilon}{2} ). Then, for ( 0 < |x - 3| < \delta ), we have: [ |(2x + 1) - 7| = 2|x - 3| < 2\delta = \varepsilon ]

Therefore, by the epsilon-delta definition of a limit, we have proved that: [ \lim_{{x \to 3}} (2x + 1) = 7 ]

Intuition

Alright, let's simplify this.

Imagine you're on a number line and you're standing at the point 3. Now, you're told to take small steps to the left or right but stay really close to 3. 

Now, there's a magic box that takes wherever you're standing, doubles that number, and adds 1. If you're standing at 3, the box gives out 7 (because \(2 \times 3 + 1 = 7\)). 

We want to show that even if you take small steps away from 3, the number that comes out of the box will always be really close to 7.

Here's how we prove it:

1. **Pick a small number, say 0.1, or any small number you like (let's call it \( \varepsilon \)).** 
This number represents how close we want the output of the box to be to 7.

2. **Now, we need to find how big of a step you can take from 3 (let's call this step size \( \delta \)) so that the box still gives a number close to 7.**
We do some math (the epsilon-delta proof) to find out that if we pick the step size (\( \delta \)) to be half of \( \varepsilon \) (the small number you picked), then the box will give out a number that is close to 7.

3. **Take small steps:** 
So if you picked \( \varepsilon = 0.1 \), then \( \delta \) will be 0.05. This means you can take steps of size 0.05 to the left or right of 3, and the box will still give out a number between 6.9 and 7.1 (which is close to 7).

This proves that as you stand close to 3, the box will always give out numbers close to 7, no matter how tiny the steps you take. And that's what the fancy math notation \( \lim_{{x \to 3}} (2x + 1) = 7 \) is saying!

Question 2

Prove that: [ \lim_{{x \to 1}} x^2 + 5x + 6 = 12 ] using the formal epsilon-delta definition of a limit.

Step 1: Plug the Limit Point into the Function
First, we plug ( x = 1 ) into the function ( f(x) = x^2 + 5x + 6 ) to find the limit ( L ): [ f(1) = 1^2 + 5(1) + 6 = 1 + 5 + 6 = 12 ]

Step 2: Set Up the Epsilon-Delta Definition
According to the epsilon-delta definition of a limit, for every ( \varepsilon > 0 ), there exists a ( \delta > 0 ) such that if ( 0 < |x - 1| < \delta ), then ( |f(x) - 12| < \varepsilon ).

Step 3: Simplify the Expression for ( |f(x) - 12| )
[ |f(x) - 12| = |x^2 + 5x + 6 - 12| = |x^2 + 5x - 6| ]

Step 4: Factor the Quadratic Expression
[ x^2 + 5x - 6 = (x - 1)(x + 6) ]

Step 5: Substitute the Factored Expression Back into the Absolute Value Expression
[ |f(x) - 12| = |(x - 1)(x + 6)| ]

Step 6: Find an Expression for ( \delta ) in Terms of ( \varepsilon )
We want to find a ( \delta ) so that ( |(x - 1)(x + 6)| < \varepsilon ) whenever ( 0 < |x - 1| < \delta ).

This is a bit tricky, but one way to approach this is to bound the expression ( |x + 6| ). If we restrict ( \delta ) to be less than or equal to 1, for example, then ( x ) will be between 0 and 2. In that case, ( |x + 6| ) will be between 6 and 8.

Step 7: Set Up the Inequality [ |(x - 1)(x + 6)| < \varepsilon ] [ |x - 1| |x + 6| < \varepsilon ]

Now, we can bound ( |x + 6| ) by 8 (the larger value) to ensure the inequality holds: [ |x - 1| \cdot 8 < \varepsilon ]

Now, solve for ( |x - 1| ): [ |x - 1| < \frac{\varepsilon}{8} ]

Step 8: Choose ( \delta )
Now we can choose ( \delta = \min\left(1, \frac{\varepsilon}{8}\right) ). This choice of ( \delta ) ensures that the inequality ( |f(x) - 12| < \varepsilon ) holds whenever ( 0 < |x - 1| < \delta ).

Conclusion:
We have demonstrated that for every ( \varepsilon > 0 ), there exists a ( \delta > 0 ) (specifically, ( \delta = \min\left(1, \frac{\varepsilon}{8}\right) )) such that if ( 0 < |x - 1| < \delta ), then ( |f(x) - 12| < \varepsilon ). Hence, by the epsilon-delta definition of a limit, ( \lim_{{x \to 1}} x^2 + 5x + 6 = 12 ).

Question 3

Prove that this limit does not exist: $\lim_{{x \to \infty}} (\cos x)$

Proof:

Objective: We want to show that the function ( \cos(\pi x) ) does not have a limit as ( x ) approaches infinity.

1. Speculating a Potential Limit ( L ):

$$L \in \mathbb{R}$$

This means we're thinking of any conceivable real number ( L ) as the possible limit of ( \cos(\pi x) ) as ( x ) goes to infinity. But, we're going to show that no such ( L ) can exist.

2. Defining a Small Positive Deviation ( \varepsilon ):

$$\varepsilon = \frac{1}{2}$$

The ( \varepsilon ) is a "buffer" we introduce. We're going to argue that ( \cos(\pi x) ) can always deviate from the speculated limit ( L ) by at least this amount, regardless of how large ( x ) is.

3. Two Clear Cases Based on ( L ): Let's discuss the nature of ( \cos(\pi x) ). It only has two possible values when ( x ) is an integer:

• 1 (for even values of ( x ))
• -1 (for odd values of ( x ))

Given this behavior, we divide our analysis into two straightforward cases based on the value of ( L ):

Case A: ( L ) is Non-negative (i.e., ( L \geq 0 ): If ( L ) is either positive or zero, then consider any odd ( x ). For such ( x ), ( \cos(\pi x) = -1 ). Hence:

$$|f(x) - L| = |-1 - L|$$

Since ( L \geq 0 ), the absolute value ( |-1 - L| ) is greater than 1. This is more than our ( \varepsilon ) buffer, meaning our function deviated from ( L ) more than we allowed.

Case B: ( L ) is Negative (i.e., ( L < 0 ): Now, if ( L ) is negative, consider any even ( x ). For such ( x ), ( \cos(\pi x) = 1 ). This leads to:

$$|f(x) - L| = |1 - L|$$

Because ( L ) is negative, the absolute value ( |1 - L| ) is again greater than 1. Our function has once more deviated from ( L ) more than the ( \varepsilon ) buffer permits.

Conclusion: Regardless of the value of ( L ) (whether it's positive, negative, or zero), the function ( \cos(\pi x) ) can always deviate from it by more than ( \varepsilon = \frac{1}{2} ) for some integer ( x ). This demonstrates that ( \cos(\pi x) ) does not have a limit as ( x ) approaches infinity.

In essence, the oscillatory behavior of ( \cos(\pi x) ) between 1 and -1 is leveraged to argue that no real number can serve as its limit as ( x ) goes to infinity.